Artist’s Horse Sketch

Goal: Convey artists’ dynamic drawing process. I.e. blocking, sketching, refining.
I’ve always loved drawing horses for their beautiful movement and figure. I’ve also been fascinated with the artistic drawing process, in which an artist begins by placing a rough sketch before refining and detailing.
Thus, using my Fourier Drawing Tool (explained below), I overlayed three versions of a full-body horse drawing to create the image above. To do this, I improved my tool by packing it into a subnet and building a UI.
I took inspiration from some of my own horse sketches, and also referenced a sketch by Salvador Dali (below, fat right).




Fourier Drawing Tool: Background
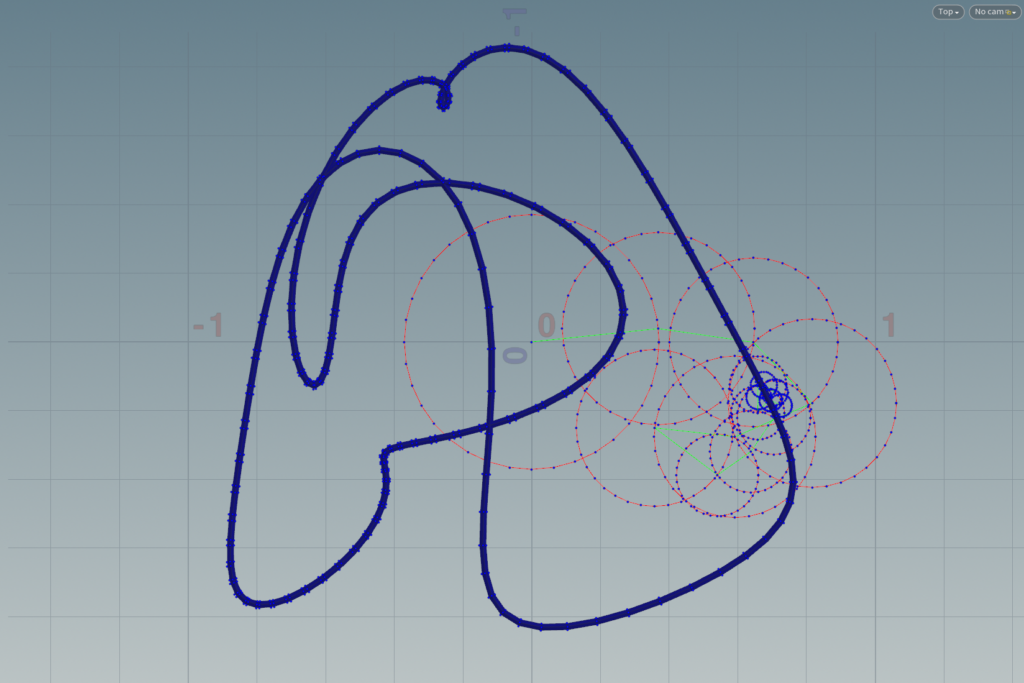
I first learned about the Discrete Fourier Transform in MATH 3130: Computational Linear Algebra (Spring 2023). Curious to learn more about its applications, I dug into 3Blue1Brown’s Fourier explanation video, which uses Fourier epicycles (rotating circles) to create line drawings.
I wanted to create my own drawing tool using the Fourier series, and this endeavor encouraged me to dive into VEX programming in Houdini. I ended up creating a tool that allows the user to input an AI vector image (the images show a horse that I drew in Adobe Illustrator), specify the number of epicycles and the speed of the drawing, and watch as circles and vectors trace the data points of the original image.
Because the number of epicycles is adjustable, the user can generate a line drawing to various degrees of specificity, resulting in some cool sketchy/abstract effects.
Breakdown


I begin by importing the AI file that I want to recreate using epicycles.
I sketched the horse to the left in Adobe Illustrator, then imported it into Houdini as a Vector file.
The AI file is then carved and resampled to clean up the drawing and evenly space out the points on the lines.
I then use an Attribute Wrangle node to program the Fourier transform summation equation and create the vectors that trace the drawing.
With a solver node, I’m able to calculate the Fourier coefficients c_i: f(t) = (C_-1)(e^(-1it)) + (C_0)(e^(0it)) + (C_1)(e^(1it)) + (C_2)(e^(2it)) + (C_3)(e^(3it)) + ….
The number of Epicycles determines the “sketchiness” of the resulting drawing. This is because fewer epicycles will oversimplify the estimation of the points on the line, whereas too many epicycles will overfit.